Для образца круглого
поперечного сечения имеет место следующая геометрическая зависимость между углом закручивания
![]() и наибольшим углом сдвига
и наибольшим углом сдвига
![]() у поверхности образца (Рис.1.4.):
у поверхности образца (Рис.1.4.):
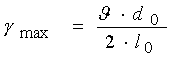 |
 (1.1) (1.1)
|
где
![]() - диаметр и длина расчётной части образца, на которой измеряется угол закручивания.
- диаметр и длина расчётной части образца, на которой измеряется угол закручивания.
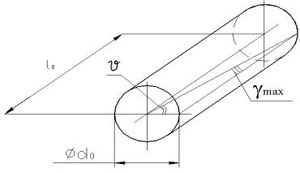
Касательные напряжения в образце круглого поперечного сечения в пределах упругости распределяются по линейной зависимости. Наибольшие касательные напряжения при кручении образца круглого поперечного сечения возникают в точках у внешней цилиндрической поверхности и в пределах применимости закона Гука вычисляются по формуле (1.2):
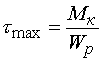 |  (1.2)
(1.2)
|
где ![]() -крутящий момент,
-крутящий момент,
![]() -полярный момент сопротивления
круглого сечения.
-полярный момент сопротивления
круглого сечения.
При кручении образца за пределом применимости закона Гука,касательные напряжения распределяются нелинейно (Рис.1.5.).
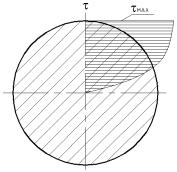
Закон распределения касательных напряжений в этом случае устанавливается в теории пластичности. наибольшие касательные напряжения при кручении сплошных цилиндрических образцов вычисляются по формуле Людвига-Кармана :
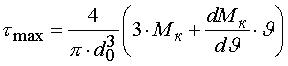 |  (1.3)
(1.3)
|